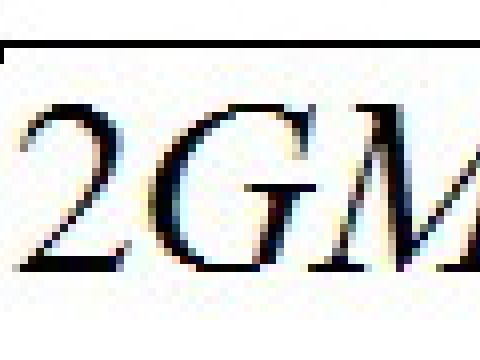Featured | Σε απόσταση 36.000km πάνω από τη Γη, κινούνται σε τροχιά οι δορυφόροι στη ζώνης Clarke, χωρίς να αλλάζουν θέση σε σχέση με τη Γη. Πώς όμως προέκυψε αυτή η απόσταση των 36.000km; Πώς γίνεται ο δορυφόρος να παραμένει «στατικός» σε αυτό το ύψος και τι αρχική ταχύτητα χρειάζεται κατά την εκτόξευση;
Γεωσύγχρονες και γεωστατικές τροχιές
Μπορεί οι παραπάνω έννοιες να χρησιμοποιούνται συχνά για να περιγράψουν την τροχιά των δορυφόρων, σαν να είναι το ίδιο πράγμα, όμως, όπως όλοι οι ορισμοί στη Φυσική, δηλώνουν κάτι απόλυτα συγκεκριμένο, πράγμα που αυτόματα σημαίνει ότι οι δύο τροχιές είναι διαφορετικές.
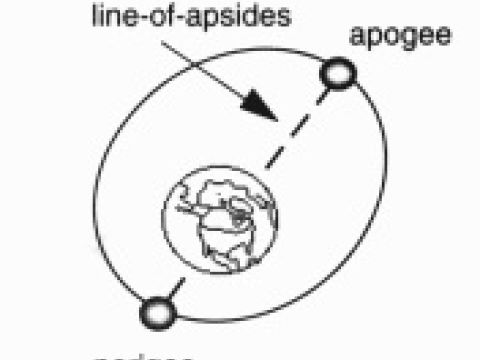
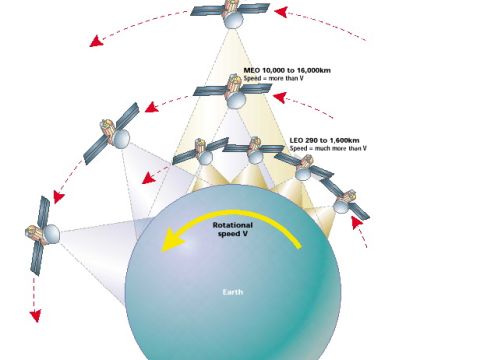
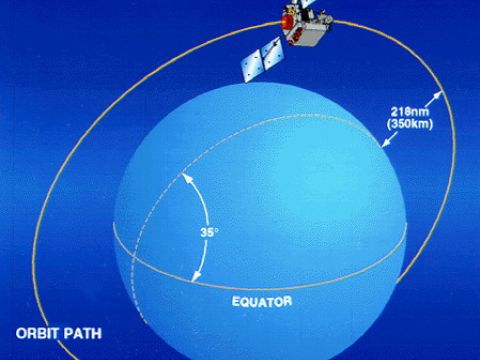
Γεωσύγχρονη ονομάζεται οποιαδήποτε τροχιά δορυφόρου, που έχει την ίδια περίοδο με την τροχιά της Γης. Η γεωσύγχρονη τροχιά μπορεί να είναι ελλειπτική και να γίνεται σε οποιοδήποτε σημείο πάνω από την επιφάνεια της Γης. Αντίθετα, η γεωστατική τροχιά είναι μια γεωσύγχρονη τροχιά, η οποία γίνεται κυκλικά, μόνο πάνω από τον Ισημερινό και αυτή είναι η τροχιά που περιγράφει την κίνηση των δορυφόρων. Στην πραγματικότητα, η αρχική τροχιά όλων των δορυφόρων είναι αρκετά ελλειπτική και η μεγαλύτερη απόσταση από την επιφάνεια της Γης ονομάζεται «απόγειο», ενώ η κοντινότερη «περίγειο». Ο σταθμός ελέγχου του δορυφόρου, υπολογίζει τη μέση απόσταση των δύο αυτών θέσεων και προσπαθεί με διορθωτικές κινήσεις να φέρει το δορυφόρο σε όσο το δυνατόν καλύτερη γεωστατική τροχιά.
Το ύψος της γεωστατικής τροχιάς
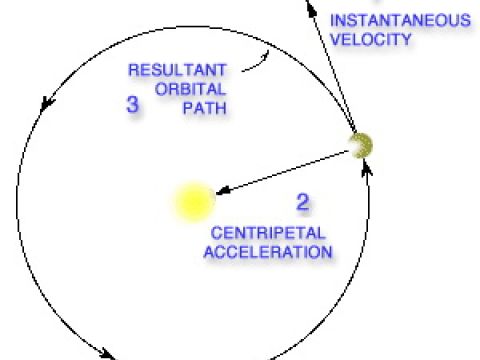
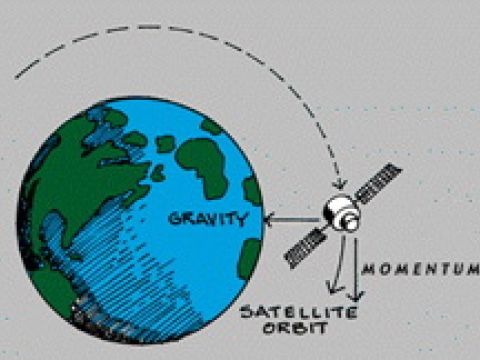
Για να μπορέσει οποιοδήποτε σώμα να εκτελέσει ομαλή κυκλική κίνηση (άρα και ο δορυφόρος), θα πρέπει η συνισταμένη των δυνάμεων που δέχεται, να έχει φορά και διεύθυνση προς το κέντρο της τροχιάς (κεντρομόλος) και να ικανοποιεί την εξίσωση ΣF=mυ2/R, όπου m είναι η μάζα του σώματος, R η ακτίνα της τροχιάς και υ η γραμμική του ταχύτητα.
Η μόνη δύναμη που δέχεται φυσικά ο δορυφόρος, είναι η βαρυτική έλξη της Γης, που δίνεται από το νόμο του Νεύτωνα. Άρα, ΣF= G Mm/R2 , όπου Μ η μάζα της Γης (Μ=5,976×1024 kg)και G η παγκόσμια σταθερά της βαρύτητας (G=6,67300 x 10-11 m3 kg-1 s-2).
Αν εξισώσουμε τις δύο παραπάνω εξισώσεις, αφού τα πρώτα μέλη είναι ίσα, έχουμε: mυ2/R = G Mm/R2. Αν απλοποιήσουμε την παραπάνω σχέση, παρατηρούμε ότι η μάζα του δορυφόρου εξαλείφεται, όπως και το τετράγωνο της ακτίνας, με αποτέλεσμα να έχουμε τη σχέση: υ2=GM/R.
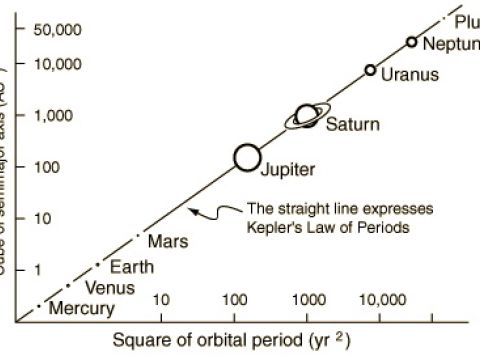
Αν τώρα αντικαταστήσουμε τη γραμμική ταχύτητα με τη σχέση υ=ωR=2πR/Τ (Τ η περίοδος της Γης), παίρνουμε τελικά 4 π2 R2/T2 = G M/R2, από την οποία παίρνουμε ότι R3=GMT2/4π2. Λύνοντας στη συνέχεια την εξίσωση ως προς R, παίρνουμε ότι R = (G M T2/4 π2)1/3. Αυτή είναι και η ακτίνα της τροχιάς ενός σώματος, που εκτελεί γεωστατική τροχιά και είναι ανεξάρτητη της μάζας του σώματος. Η εξίσωση αυτή δεν είναι τίποτα άλλο, από τον τρίτο νόμο του Kepler. Φυσικά, οι εξισώσεις υπολογίστηκαν από το κέντρο της Γης (που είναι και το κέντρο της τροχιάς), επομένως, αν επιθυμούμε να υπολογίσουμε το ύψος, θα πρέπει να αφαιρέσουμε από το νούμερο αυτό την ακτίνα της Γης, δηλαδή Η=R-Rγ. Αντικαθιστώντας τις τιμές των σταθερών στις εξισώσεις, παίρνουμε ότι Η= 35.786km και αυτό είναι το ακριβές ύψος που πρέπει να βρεθεί οποιοδήποτε σώμα, για να εκτελέσει γεωστατική τροχιά γύρω από τη Γη ή, αν προτιμάτε, μαζί με τη Γη, αφού σε αυτήν την απόσταση, το σώμα δεν θα αλλάζει θέση, σε σχέση με την επιφάνεια της Γης.
Ταχύτητα διαφυγής και τροχιακή ταχύτητα
Όλοι γνωρίζουμε ότι με όση ανθρώπινη δύναμη κι αν ρίξουμε μια πέτρα προς τα επάνω, αυτή θα γυρίσει στην επιφάνεια της Γης. Έχουμε όμως καταφέρει να εκτοξεύσουμε αρκετά σώματα, τα οποία μπόρεσαν να ξεφύγουν από το βαρυτικό πεδίο της Γης και να βγουν στο διάστημα. Για να συμβεί αυτό, θα πρέπει η κινητική ενέργεια του σώματος που εκτοξεύουμε, να είναι μεγαλύτερη ή το πολύ ίση, με τη δυναμική ενέργεια του βαρυτικού πεδίου της Γης, στην επιφάνεια της γης, δηλαδή, θα πρέπει
Εκ=Εδ (τουλάχιστον ίση), άρα
mυ2/2 = GMm/Rγ. Κι εδώ απλοποιείται η μάζα κι αν λύσουμε ως προς
υ παίρνουμε:
Η ταχύτητα αυτή, ονομάζεται ταχύτητα διαφυγής και ισούται με 11,1km/sec (40.200km/h) και είναι η ελάχιστη ταχύτητα που πρέπει να έχει ένα σώμα, για να ξεφύγει από τη βαρυτική επίδραση της Γης.
Εμείς όμως, δεν θέλουμε να δώσουμε ταχύτητα διαφυγής στους δορυφόρους, αλλά αρκετά μικρότερη, αφού πρέπει απλά να «ισορροπήσουν» σε ένα συγκεκριμένο ύψος. Αυτή η ταχύτητα ονομάζεται τροχιακή ταχύτητα και είναι, φυσικά, η γραμμική ταχύτητα που θα έχει ο δορυφόρος κατά την περιστροφή. Στην πραγματικότητα, όταν το διάνυσμα αυτής της ταχύτητας γίνει κάθετο με το διάνυσμα της κεντρομόλου, τότε το σώμα θα αρχίσει να εκτελεί κυκλική τροχιά, στο συγκεκριμένο ύψος. Αφού όμως τώρα, ξέρουμε το ύψος, αν λύσουμε την εξίσωση της προηγούμενης παραγράφου mu2/R = G Mm/R2. ως προς υ, παίρνουμε την απάντησή μας . H ταχύτητα αυτή υπολογίζεται στα 3,07km/sec, περίπου 4 φορές μικρότερη από την ταχύτητα διαφυγής. Αυτή είναι λοιπόν περίπου η ταχύτητα εκτόξευσης, που χρειάστηκαν ο Hotbird, o Astra και ο Hellas Sat, για να τοποθετηθούν στις τροχιακές θέσεις 13Ε, 19,2Ε και 39Ε αντίστοιχα. Και λέμε περίπου, γιατί στους υπολογισμούς μας δεν συνυπολογίσαμε την απώλεια λόγω τριβών στην ατμόσφαιρα, τις διορθωτικές κινήσεις των δορυφόρων και θεωρήσαμε σαν παραδοχή μια τέλεια γεωστατική τροχιά.
Εκτιμούμε όμως, ότι σήμερα δεν είναι η μέρα όπου σκοπεύετε να εκτοξεύσετε το δορυφόρο σας, οπότε μπορείτε να αρκεστείτε στους λειψούς αυτούς υπολογισμούς…